¿Cuántos resultados significativos esperamos por azar?

Notas del autor: las palabras seguidas de un superíndice tienen al final de esta página un comentario asociado; los términos en negrita y cursiva aparecen descritos casi al final de la página en un glosario.

Prólogo

En una cafetería imaginaria, de una universidad imaginaria, una bioestadística imaginaria espera a su colega imaginario mientras bebe un doppio^[1] imaginario.

Erica: ¡Hola Pancho! Que bueno que alcanzaste a llegar.
Pancho: Hola Erica, disculpa la demora.
Erica: Nah, tranquilo. Es un gusto verte, y el café está muy bueno hoy… ¿Cómo estás?
Pancho: Jeje, gracias Eri. Yo bien. Un poco distraído sí. ¿Y tú?
Erica: Bien también, pero ya sabes, inicio de semestre.
Pancho: Uf, sí, que atroz…
Erica: Jaja, bueno, tampoco es para tanto. ¿Y qué te tiene distraído esta vez?
Pancho: Una cuestión que no pude aclarar al equipo colaborador de ciencias de la salud.
Erica: ¿Qué cuestión?
Pancho: “El problema de Bonferroni”.
Erica: ¿Ah?
Pancho: Este problema que surge cuando se realizan muchas pruebas estadísticas de forma simultánea—^[2]
Erica: Ahh, el problema de comparaciones o pruebas múltiples, o simplemente problema de multiplicidad.
Pancho: ¡Ese mismo! El investigador principal quiere realizar una prueba de hipótesis de asociación estadística entre un fenotipo y genotipo, ¡pero como para 100 loci^[3] a la vez!

Pruebas de hipótesis según Fisher

Un adulto imaginario les trae un cappuccino vainilla^[4] imaginario a la mesa imaginaria.

Adulto: Su café.
Pancho: ¿Oh?
Erica: Gracias, Don Gabriel. Pedí tu favorito, Pancho.
Pancho: Ay, Eri, eres un amor conmigo.
Erica: Jaja, tranqui, Pancho, el próximo lo invitas tú.
Pancho: Bueno. ¿Podrías explicarme el problema de la multiplicidad de pruebas con tus palabras? Tú explicas mucho mejor que yo, jeje…
Erica: Uf, bueno, bueno… veamos. Primero el contexto. Imaginemos que queremos evaluar varias hipótesis científicas y que para ello haremos una docimasia de hipótesis—
Pancho: ¿Docimasia? Dí prueba de hipótesis^[5] no más.
Erica: Bueno ya, pero no me interrumpas, ¿vale? Entonces, como iba diciendo, haremos una prueba de hipótesis estadística para cada hipótesis científica que deseemos evaluar.
Pancho: Ajá, y si seguimos el enfoque de Fisher fijamos cierto valor para definir que un resultado sea estadísticamente significativo—
Erica: Con respecto a una hipótesis nula, estadísticamente significativo con respecto a una hipótesis nula.
Pancho: Exacto, una hipótesis estadística nula, H₀,^[6] bajo la cual el estadístico de prueba tendrá una distribución de muestreo conocida.
Erica: Gracias por complementar la explicación que me habías pedido hacer a mí. ¿Quieres continuar tú o sigo yo?
Pancho: Jaja, lo siento. Mala costumbre mía. Continúa, por favor.
Erica: Bueno. Entonces digamos que tal valor, el nivel de significación estadística, α,^[7] es igual al típico 0,05 que tanto les gusta—
Pancho: Ay, sí, ese cinco por ciento.
Erica: Sí, que les encanta a los equipos colaboradores. En fin. Si el p-valor es menor que ese 0,05, rechazamos H₀ y decimos que observamos un resultado estadísticamente significativo.
Pancho: Ajá.
Erica: Esto implica que, en cada prueba donde H₀ sea verdadera, tendremos una probabilidad igual a α de que obtengamos una muestra que nos lleve a declarar un resultado estadísticamente significativo.
Pancho: ¡Pese a que es falso!
Erica: Sí po, pese a que es falso. Eso sería un error de tipo I si quisiéramos usar la jerga de Neyman y Pearson.
Pancho: ¿Pearson padre o hijo?
Erica: Mmm… no recuerdo. Pero no importa.
Pancho: No querríamos que nuestros estudiantes dijeran eso sobre nuestros libros.
Erica: Jajaja, da igual, ni que nos fueran a citar alguna vez…

El problema de la multiplicidad de pruebas

Pancho busca rápidamente la respuesta en su celular imaginario.

Pancho: ¡Hijo! es Pearson hijo—
Erica: Ah, estoy segura que lo olvidaré, jaja.
Pancho: Yo igual, pero bueno, ¿y el problema?
Erica: Ninguno, no me interesa la fama.
Pancho: Jaja, no, no. El problema de la multiplicidad de pruebas.
Erica: Ah, sí, jaja. Verdad que a eso íbamos. Entonces, si hacemos, digamos, 20 pruebas de hipótesis. ¿Cuál sería la probabilidad de que, siendo las veinte H₀ verdaderas, obtengamos al menos un resultado estadísticamente significativo?
Pancho: Depende.
Erica: ¿De qué depende?
Pancho y Erica: De según como se mire, todo depende. Jajaja…
Pancho: ¿Son estadísticamente independientes entre sí?
Erica: ¿Las pruebas? supongamos que sí, para que sea más fácil de calcular.
Pancho: Pues, uf… a ver, suponiendo eso… sería el complemento de la probabilidad de que no ocurra ningún resultado significativo en las 20 pruebas. Uno menos 0,95 a la 20, ni idea cuanto es eso.^[8]
Erica: Es como 64% o algo así.
Pancho: ¡Mucho más grande que 0,05!
Erica: Sí, aunque no es directamente comparable a α, por eso a este 0,64 le llaman family wise error rate.
Pancho: Oh my! is that the, whatchamacallit, FWER? jaja, tan gringa que saliste Erica.
Erica: Jajaja, ¡pesa’o! la tasa de error… ¿familiar? no creo que sea así en castellano, no me suena bien.
Pancho: I agree, my dear. Pero ya llegamos a lo que queríamos llegar.
Erica: Así es. El problema de la multiplicidad de pruebas es que si hacemos muchas pruebas estadísticas entonces las chances de que terminemos con al menos un resultado signi— digo, estadísticamente significativo, va a ser muuyyy alta.
Pancho: ¡Y eso era lo que intentaba explicarle al equipo colaborador! Imagínate que querían hacer como 100 pruebas estadísticas. Te encargo la “efewer”.^[9]
Erica: Jaja, “efewer”. Pero sí po, “me muera” con esa FWER.
Pancho: Yo igual. Pero no hubo caso.
Erica: Mmm… ¿Sabes? se me ocurre una forma en que podrías convencerles.
Pancho: ¿¡Sí!? Sabía que se te ocurriría algo, te escucho.
Erica: ¿Y si les muestras un gráfico de la distribución de muestreo del número de resul—
Gabriel: Disculpen por interrumpirles, pero ya estamos por cerrar.
Erica: Oh, disculpe. No nos dimos cuenta de la hora. Pagamos y nos vamos, Don Gabriel.
Pancho: ¿Oye, y si vamos a los cubículos? No quiero quedarme con las ganas.
Erica: Tú siempre me dejas con ganas.
Pancho: Shooaaa~ jaja, vamos, no seas mala.
Erica: Bueno ya, pero compremos unos cafés y algo de comer para llevar.
Pancho: ¡Me gusta la idea! Yo invito.
Erica: Me parece.

Otra forma de ver el problema de la multiplicidad de pruebas

Erica y Pancho se sientan frente al computador imaginario en el cubículo imaginario de Erica, con sus cafés imaginarios y sus donas veganas imaginarias.

Erica: Te decía que podrías mostrarles un gráfico de la distribución de muestreo del número de resultados que se declaran como estadísticamente significativos.
Pancho: ¿Ajá?
Erica: Sólo tendrías que suponer un número de pruebas a realizar, por ejemplo 100, elegir un α, digamos que igual a 0,05, y suponer que en realidad todas las 100 H₀ son verdaderas.
Pancho: Suena bien, ¿pero cuál es esa distribución de muestreo?
Erica: Veamos… si cada prueba es independiente de las demás, y tenemos un 5% de que cada prueba dé un resultado significati— ¡Ah! es una distribución binomial.
Pancho: Pff, verdad.
Erica: Parece que estamos apenas con el café y las donas, jaja.
Pancho: Hagamos el gráfico entonces,^[10] antes que se nos eche la yegua…
Erica: Ya se nos echó. Aquí está.^[11]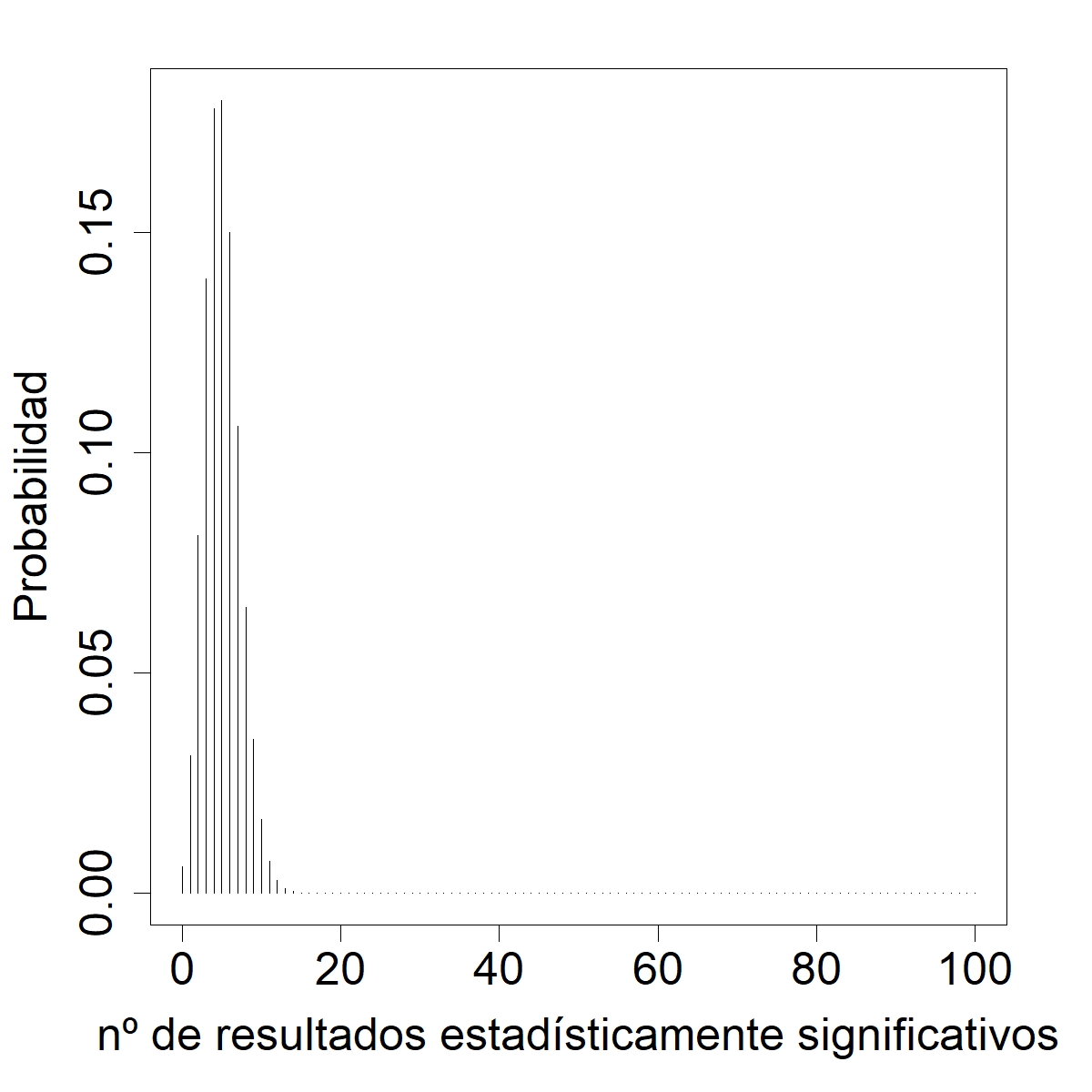Pancho: Baia baia…
Erica: Mmm… ¿hagámosle zoom?^[12]

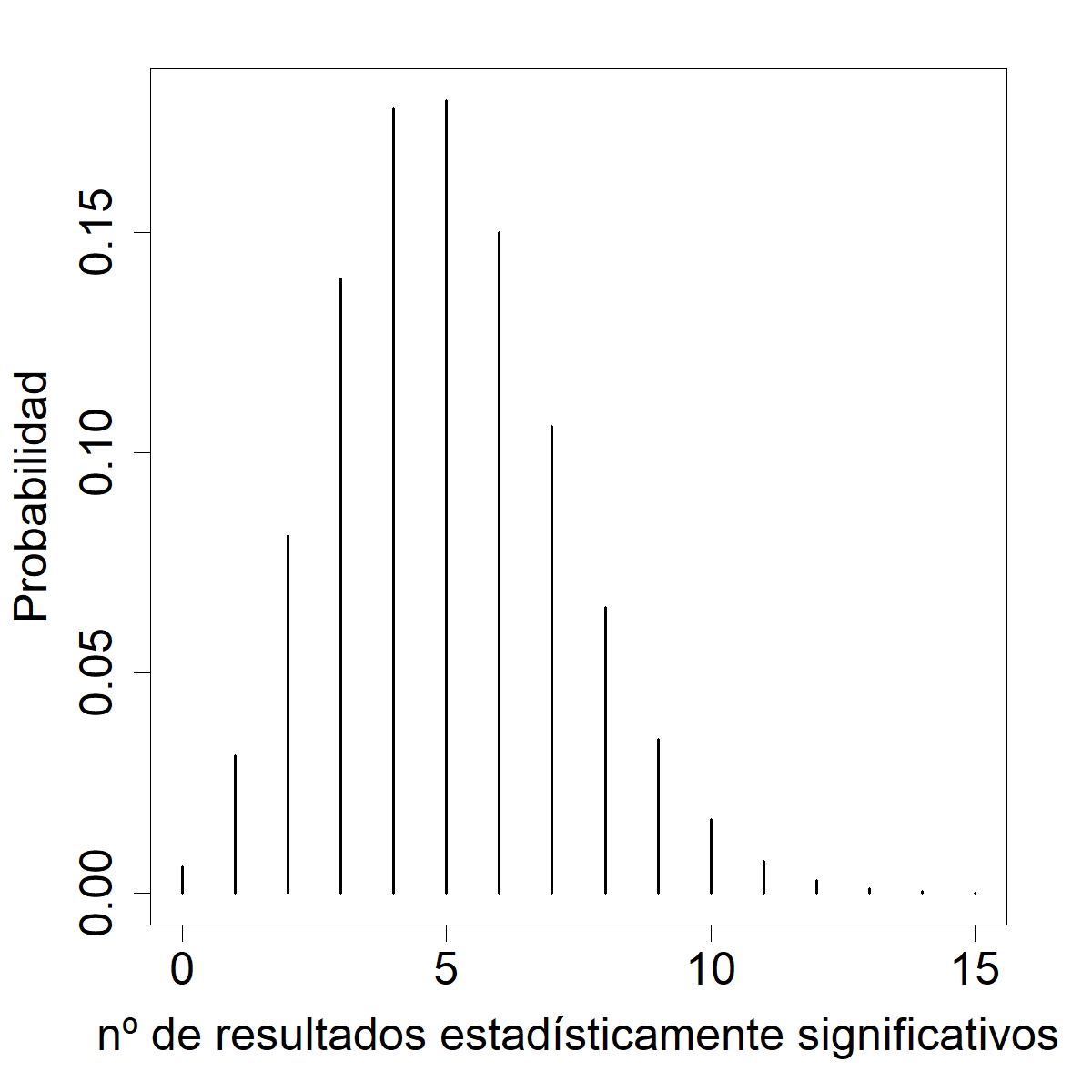
Pancho: Fuuaaa. Eres seca, Eri.
Erica: Lo sé, jaja. Pero cuático, ¿no?
Pancho: La cag— digo, la embarró. Es casi seguro que se obtendrá al menos un falso positivo.
Erica: ¿“Casi seguro”? No nos metamos en teoría de la medida por favooor.
Pancho: Jaja, sabes a lo que me refiero.
Erica: Sí sé, jeje. Mira, de hecho la probabilidad de observar al menos un resultado estadísticamente significativo es 0,994 po.^[13]
Pancho: Cónchale vale…
Erica: Y la probabilidad de… esto, hay un 90% de probabilidad de que se declaren de 2 a 8 resultados como estadísticamente significativos,^[14] ¡pese a que todas las hipótesis nulas eran verdaderas!
Pancho: Gracias, Eri. Esto debería bastar para convencer al equipo colaborador.
Erica: Ojalá, Pancho… Ya, ¿nos vamos? Que seguro mis Luisa y Julia aún no cenan.
Pancho: Típico de las crías. Ya, vámonos ¿Tomas el metro?
 

Epílogo

En una sala de reuniones imaginaria, Pancho y el equipo colaborador discuten el plan de análisis estadístico del proyecto imaginario en que trabajan.

Pancho: Y por esto no sería correcto usar ese nivel de significación estadística para decidir si un valor de p indica o no que el resultado fue estadísticamente significativo. ¿Alguna pregunta?
Investigador principal: No, Pancho. Nos ha quedado bastante claro.
Coinvestigadora: Así es. ¿Entonces deberíamos ajustar α para que la tasa de error familiar esté controlada?
Pancho: Exactamente. Una corrección sencilla es usar el resultado de dividir el α, que se usaría para una sola prueba, por el número de pruebas.
Coinvestigadora: Muy bien, entonces sería 0,05 entre 100… ¿0,0005?…
Pancho: Exacto.
Tesista: Disculpen, ¿pero eso no sería un umbral muy pequeño? Creo que es muy raro ver un p-value tan chico. Incluso para algunas asociaciones ya confirmadas como causales se han observado p-values más grandes.
Investigador principal: ¿Es verdad?
Coinvestigadora: Ahora que lo dice, 0,0005 es realmente pequeño comparado con lo que vemos en otros papers.
Tesista: Disculpen otra vez, ¿pero y si además las pruebas no son independientes entre sí?
Investigador principal: Ohh, cierto ¿Qué podemos hacer en esos casos, Pancho?
Pancho: Ehh… Bueno, hay otros métodos para corregir este problema que surge por hacer demasiadas pruebas estadísticas.
Investigador principal: ¿Ajá?
Pancho: Mmm, ehh… Veamos, ahora mismo recuerdo el método de Tukey, el de “Benjamín-Hogberg”,^[15] y el de la tasa de descubrimientos falsos o “efe-de-erre”.^[16]
Tesista: Ese último me suena.
Coinvestigadora: ¿Sí? a mí sólo me suena el primero ahora que hago memoria ¿El de Tukey no se usaba después de hacer un ANOVA?
Investigador principal: Parece que sí. ¿Pancho, podría explicarnos de qué tratan estos tres métodos alternativos?
Pancho: Ehh, sí, claro…
Investigador principal: ¿Ajá?...
Pancho: Pero no vine preparado ¿Y si lo dejamos para la próxima reunión?
Equipo colaborador: ¡plop!
________________________________

Agradecimientos.
Por leer el borrador de este diálogo y motivarme a enviarlo: Felipe Santibañez, Francisco Medina, Rodrigo Lagos, y Sergio Alvarado. Por revisar y sugerir mejoras al escrito: Cristian Moya, Mauricio Fuentes, y Marco Medina. Cualquier erorr que haya quedado es pura responsabilidad del autor.
________________________________

Referencias recomendadas

Altman, Naomi, y Krzywinski, Martin (2017) P values and the search for significance. Nature Methods 14, 3–4. doi: 10.1038/nmeth.4120
Krzywinski, Martin, y Altman, Naomi (2014) Comparing samples—part II. Nature Methods 11, 355–356. doi: 10.1038/nmeth.2900
Perezgonzalez, Jose D. (2015) Fisher, Neyman-Pearson or NHST? A tutorial for teaching data testing. Frontiers in Psychology 6:223. doi: 10.3389/fpsyg.2015.00223
________________________________

Glosario estadístico

• ANOVA. Sigla en inglés para análisis de la varianza, es un método estadístico utilizado para inferir acerca de las medias de dos o más grupos a partir de muestras aleatorias provenientes de cada grupo. La hipótesis nula es que las medias de todos los grupos son iguales. La inferencia se realiza en base al cociente entre dos estimadores diferentes de la varianza del error de medición. Cuando se cumplen los supuestos del modelo, el estadístico de prueba distribuye F de Fisher-Snedecor.
• Casi seguro. En teoría de probabilidades un evento es casi seguro (u ocurre casi seguramente) cuando su probabilidad es 1. En general, cualquier evento será casi seguro si su complemento está contenido en (o es) un evento con medida de probabilidad nula. Este concepto es aplicado, por ejemplo, en la noción de convergencia casi segura usada en la ley fuerte de los grandes números. Por último, la teoría de probabilidades es un caso particular de teoría de la medida, donde “casi en todas partes” es el análogo de “casi seguro”.
• Distribución binomial. La distribución del número de éxitos (S) que resulta de realizar un número fijo (n) de experimentos aleatorios que son estadísticamente independientes entre sí, cada uno con dos posibles resultados (éxito,X_i=1; fracaso, X_i=0), y una probabilidad fija de que un experimento resulte en un éxito (i.e.Pr(X_i=1)=π). La distribución de S se denomina “distribución binomial” y tiene valor esperado nπ y varianza nπ(1-π).
• Distribución de muestreo. La distribución de un estadístico. Como un estadístico es una función de una o más variables (o cantidades) aleatorias, éste también será una cantidad aleatoria y por tanto tendrá una distribución de probabilidad. Las distribuciones de muestreo son importantes porque pueden ser utilizadas para, por ejemplo, proponer estimadores o pruebas de hipótesis.
• Error de tipo I. Concepto del enfoque de Neyman y Pearson. Corresponde al evento en el que, pese a que la hipótesis nula es verdadera, la muestra aleatoria observada nos ha llevado a tomar la decisión de rechazar la hipótesis nula. En el enfoque de Neyman y Pearson se controla la probabilidad de tal error, i.e. la tasa de cometer un error de tipo I, la cual suele ser simbolizada con la letra .
• Estadísticamente independientes. Dos o más eventos que tienen probabilidades de ocurrir que no están influenciadas por la ocurrencia o no de los demás eventos. Por ejemplo, si A y B son eventos estadísticamente independientes, entonces Pr(A|B)=Pr(A) y Pr(B|A)=Pr(B). Lo anterior es relevante porque significa que Pr(A∩B)=Pr(A|B)Pr(B)=Pr(A)Pr(B).
• Estadísticamente significativo. Se suele declarar que un resultado de un análisis inferencial es estadísticamente significativo cuando el p-valor es menor que cierto valor de referencia (en el enfoque de Fisher) o cuando se decide rechazar la hipótesis nula (en el enfoque de Neyman y Pearson). No se debe confundir con la significancia práctica de los resultados, la cuál debe basarse en criterios del área donde la metodología estadística es un apoyo auxiliar al método científico.
• Family wise error rate. Corresponde a la tasa de error de tipo I para una familia (o grupo) de pruebas de hipótesis que se realizan de manera simultánea. Si la hipótesis nula es que ninguna de las hipótesis nulas es cierta, entonces la hipótesis alternativa es que al menos una de esas hipótesis nulas es verdadera. El problema entonces es que esta tasa de error no coincide con la tasa de error tipo I de una prueba de hipótesis aislada. Esto puede llevar a que resultados aparentemente significativos desde un punto de vista estadístico, sean realmente falsos positivos.
• Fisher. Sir Ronald Aylmer Fisher (estadístico y biólogo inglés, nacido en 1890, fallecido en 1962). Propuso un enfoque de pruebas de hipótesis influenciada por el falsacionismo Popperiano y basado en la cuantificación de la fuerza de la evidencia en el p-valor. Gran parte del método se puede desarrollar a priori o a posteriori de la obtención de los datos. Lo anterior hace que el procedimiento tenga un carácter más bien exploratorio que confirmatorio. A diferencia del enfoque de Neyman y Pearson, no hay una hipótesis estadística alternativa explícita, y la falta de evidencia en contra de la hipótesis nula no implica que haya evidencia a favor de ella, por lo que un resultado que no se declara como estadísticamente significativo es uno que no es concluyente respecto a la hipótesis nula.
• Hipótesis nula. También llamada hipótesis de nulidad (por nulidad del efecto), es una hipótesis estadística que contradice a la hipótesis de investigación. La hipótesis estadística hace referencia a las propiedades del modelo estadístico supuesto, como la dependencia estadística, la distribución de las cantidades aleatorias, o los parámetros de tales distribuciones. La contradicción entre ambas hipótesis se debe a la influencia del filósofo Karl Popper sobre quienes propusieron métodos para llevar a cabo pruebas de hipótesis estadísticas. Según el falsacionismo popperiano, y en términos muy simples, no hay cantidad de evidencia que pueda comprobar una hipótesis, pero sí refutar. Otro argumento a favor de usar una hipótesis estadística que contradice a la hipótesis de investigación es que ésta podría implicar una distribución de muestreo del estadístico de prueba que sea conocida o fácil de aproximar.
• Neyman y Pearson. Jerzy Neyman (matemático y estadístico polaco, nacido Jerzy Spława-Neyman en 1894, fallecido en 1981) y Egon Sharpe Pearson (estadístico británico, nacido en 1985, fallecido en 1980). Propusieron un enfoque de pruebas de hipótesis basado en teoría de decisiones, donde la evidencia muestral se utiliza para sopesar entre dos hipótesis estadísticas complementarias (las hipótesis nula y alternativa). Gran parte del método se desarrolla a priori del análisis de los datos, ya que requiere de una planificación que mantenga bajo control la tasa de cometer un error de tipo I (rechazar una hipótesis nula, a favor de la alternativa, cuando la hipótesis nula es cierta) y un error de tipo II (rechazar una hipótesis alternativa, a favor de la nula, cuando en realidad la hipótesis alternativa es cierta). Este enfoque permite tomar una decisión con respecto a la hipótesis nula: aceptarla o rechazarla. Si bien esto no implica que la hipótesis de investigación sea cierta o no, el resultado aporta evidencia a favor o en contra de ella, sirviendo las tasas de error de tipo I y tipo II como indicadores del riesgo de tener la mala suerte de analizar una muestra cuya evidencia vaya en contra de la hipótesis que es en realidad verdadera.
• Nivel de significación estadística. En el enfoque de Fisher corresponde a un umbral que indica si un resultado observado es estadísticamente significativo. Si bien puede ser definido a priori, en el enfoque de Fisher el p-valor es usado como un indicador del peso de la evidencia, lo que está más en línea con un procedimiento exploratorio que uno resolutivo en el que se toma la decisión de aceptar o rechazar una hipótesis estadística nula (c.f. enfoque de Neyman y Pearson).
• p-valor. Es un estadístico, al ser una función de la muestra aleatoria, clave en el enfoque de Fisher. Corresponde a la probabilidad de observar un resultado tanto o más contradictorio con la hipótesis estadística nula que lo obtenido en la muestra aleatoria observada, condicional a que tal hipótesis es verdadera. Un valor pequeño indicaría que se observó un evento muy improbable si la hipótesis nula fuera verdadera, por lo que la muestra presentaría evidencia en contra de tal hipótesis.
• Prueba de hipótesis (estadística(s)). Es una metodología de estadística inferencial que busca apoyar en la cuantificación de la evidencia o toma de decisiones con respecto a una o más hipótesis estadísticas. El enfoque presentado en textos introductorios utilizados en pregrado suele ser una amalgama entre el enfoque de Fisher y el de Neyman y Pearson. Lo anterior puede generar algunas inconsistencias en la interpretación de algunos resultados o, peor aún, inducir prácticas erróneas (e.g. aceptar una hipótesis nula cuando no se ha controlado la tasa de error tipo II, calcular post hoc la potencia estadística de la muestra).
  ________________________________

[1] Un doppio es un café espresso hecho con dos cargas, extraído utilizando un filtro de café doble.​​​ Esto resulta en una bebida con el doble del volumen de un espresso convencional.
[2] Estas rayas simbolizan interrupciones. Por ejemplo, aquí Erica interrumpe a Pancho.
[3] Loci es el plural de locus. Un locus es un lugar en un cromosoma donde podría haber algún hito genético de interés (e.g. un gen, un polimorfismo).
[4] Un cappuccino vainilla es un cappuccino con un shot de vainilla, y un cappuccino es un espresso con leche montada con vapor para darle cremosidad.
[5] Los términos en negrita y cursiva aparecen descritos casi al final de la página en un glosario.
[6] Deberíamos llamarle “hache sub-cero”, pero solemos llamarle “hache-cero” por cariño.
[7] α es la minúscula de la letra griega alfa.
[8] 1 - 0,95²⁰ ≈ 0,6415.
[9] Debería leerse la sigla FWER en español o inglés, y ninguna suena como “efewer”.
[10] Para reproducir el aspecto de las figuras deberá ejecutar antes en R: par(mar = c(5,4,2,2)+0.1, pty = "s", ps = 20)
[11] En R: plot(y = dbinom(x = 0:100, size = 100, prob = 0.05), x = 0:100, type = "h", xlab = "nº de resultados estadísticamente significativos", ylab = "Probabilidad")
[12] En R: plot(y = dbinom(x = 0:100, size = 100, prob = 0.05), x = 0:100, type = "h", xlab = "nº de resultados estadísticamente significativos", ylab = "Probabilidad", xlim = c(0,15), lwd = 2)
[13] En R: pbinom(q = 0, size = 100, prob = 0.05, lower.tail = FALSE)
[14] En R: sum(dbinom(x = 2:8, size = 100, prob = 0.05))
[15] Procedimiento de Benjamini-Hochberg.
[16] False discovery rate (FDR).